等距缩放多边形
0x0. 问题
假定存在一个多边形（不论凹凸），先需要对这个多边形进行缩放以生成新的多边形，这里的缩放分为两种情形：
- 缩放后，新多边形的所有顶点与原顶点的距离一致，如以下情况
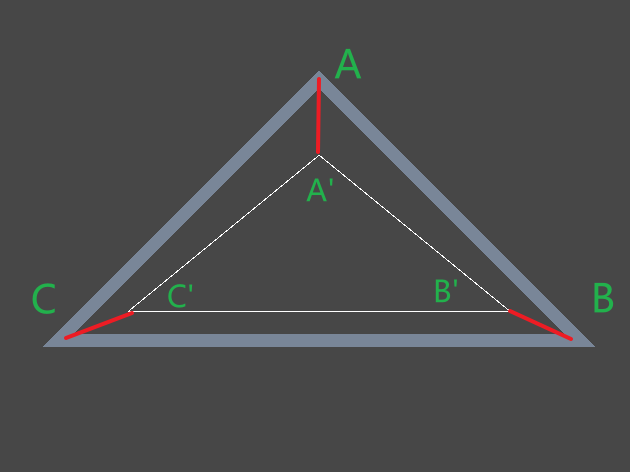多边形ABC与缩放后的多边形A’B’C’保持了|AA’| = |BB’| = |CC’| - 缩放后，新多边形的轮廓与原轮廓距离一致，如下图所示，这种情况称为等距缩放。
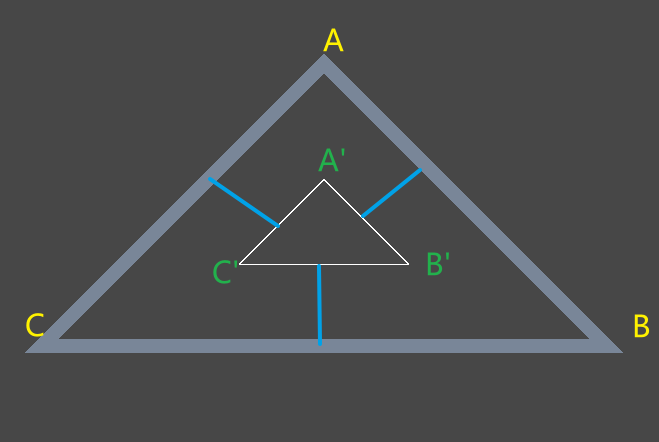
0x1. 实现
在说明实现之前，先给定多边形的定义，多边形（Polygon）由一系列2D平面上的点组成，这些点首尾相连组成的封闭图形称为多边形。
Polygon(A) = { PointA, PointB, ... }
对于多边形中的某一点A，需要计算其缩放距离d之后的新位置A'，缩放后的距离只要求出移动的方向与移动距离即可算出A'的位置。
对于缩放方向，考虑其相邻的两个点P和N，计算其法线NN和NP，则缩放的方向即为Normalize(NN + NP)。
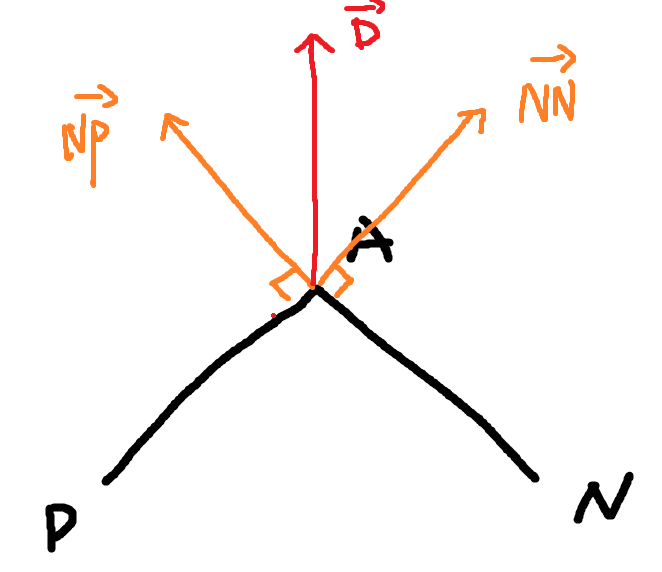对于单位二维向量(x, y)，法线易求得为x + y = 0，取决于方向，法线向量可以为(-y, x)或者(y, -x)。
若求顶点距离一致的缩放多边形，则新顶点位置为A' = Normalize(NN + NP) * d，其代码实现如下：
Vector2[] Expand(Vector2[] points, float offset)
{
int count = points.Length;
Vector2[] result = new Vector2[count];
for (int cur = 0; cur < count; ++cur)
{
int prev = (cur + count - 1) % count;
int next = (cur + 1) % count;
// 下一邻接点的法线
Vector2 pNext = (points[next] - points[cur]).normalized;
Vector2 nextNormal = new Vector2(-pNext.y, pNext.x);
// 上一邻接点法线
Vector2 pPrev = (points[cur] - points[prev]).normalized;
Vector2 prevNormal = new Vector2(-pPrev.y, pPrev.x);
// 等分线
Vector2 bis = (nextNormal + prevNormal).normalized;
// 顶点距离一致
result[cur] = points[cur] + bis * offset;
}
return result;
}
若要求等距缩放，则计算会复杂一些，如下图所示
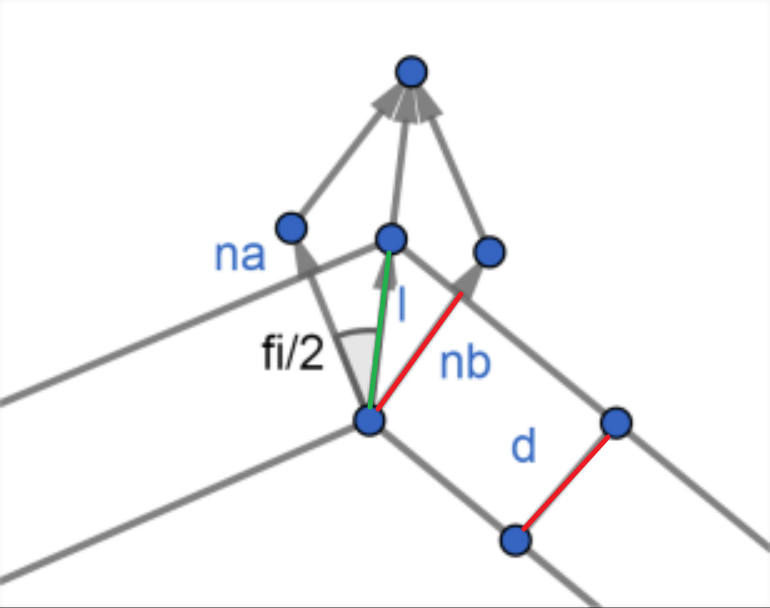已知红色部分长度相同，均为缩放距离d，na与nb为点A与其邻接点的法线，缩放方向仍然为上述计算得出的方向，只是距离变成了途中绿色部分长度l，法线间夹角为fi，则显然有
cos(fi/2) = d/l，
根据半角公式，有
sqrt((1+cos(fi)) / 2) = d / l，
由于na与nb均为方向向量，有
cos(fi) = dot(na, nb)，
代入上式得
l = d / sqrt((1 + dot(na, nb)) / 2)
则新点A' = A + bis * l，其代码实现如下：
Vector2[] Expand(Vector2[] points, float offset)
{
int count = points.Length;
Vector2[] result = new Vector2[count];
for (int cur = 0; cur < count; ++cur)
{
int prev = (cur + count - 1) % count;
int next = (cur + 1) % count;
// 下一邻接点的法线
Vector2 pNext = (points[next] - points[cur]).normalized;
Vector2 nextNormal = new Vector2(-pNext.y, pNext.x);
// 上一邻接点法线
Vector2 pPrev = (points[cur] - points[prev]).normalized;
Vector2 prevNormal = new Vector2(-pPrev.y, pPrev.x);
// 等分线
Vector2 bis = (nextNormal + prevNormal).normalized;
// 等距缩放距离
float len = offset / Mathf.Sqrt((1 + Vector2.Dot(nextNormal, prevNormal)) / 2f);
result[cur] = points[cur] + bis * len;
}
return result;
}
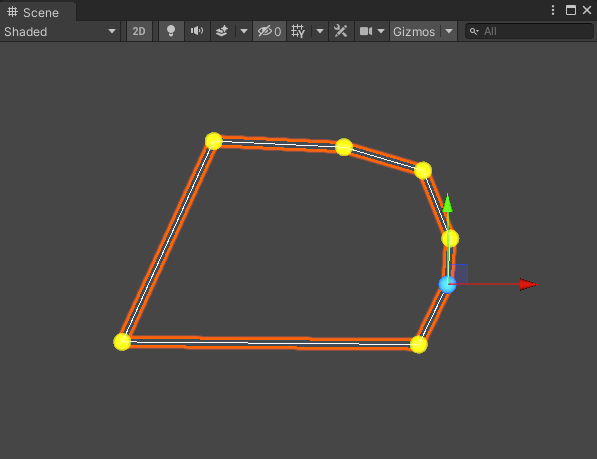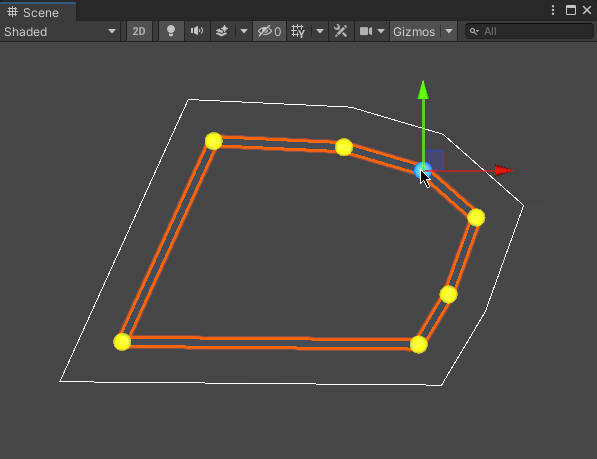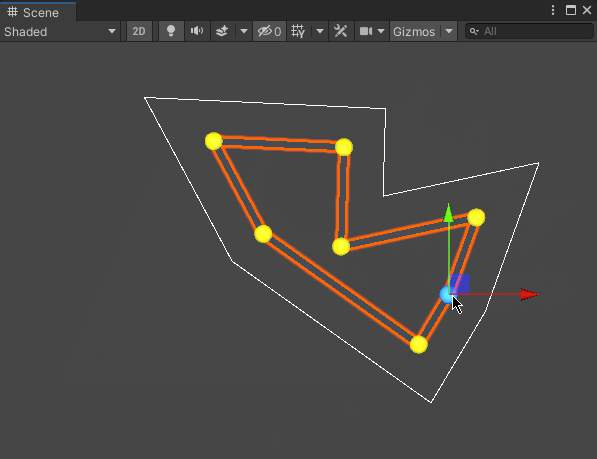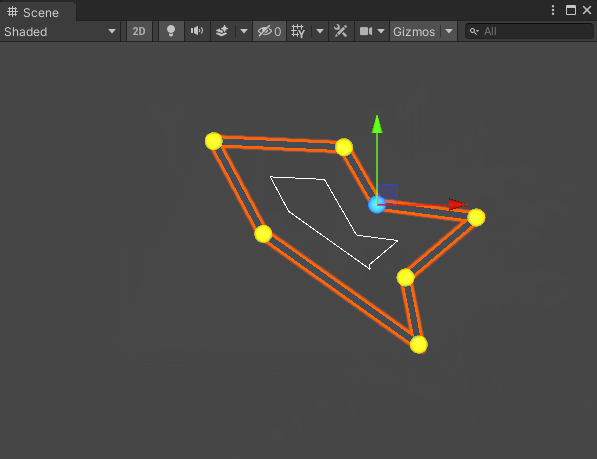
0x2. 效果
